Probabilistic Adjudication: Part III - clashes and metrics

What is this mini-series about?

The overall purpose of these posts is to build a framework to judge debates probabilistically and illustrate how some parts of adjudication work within this framework. Part I dealt with a single argument made by a team in a vacuum. Part II dealt with direct interaction between two teams through rebuttal and extensions. This part deals with the comparison between different teams along different metrics. As already emphasized in the first part, I want these posts to be as understandable as possible even for people that do not have any background in statistics or math. If you do not understand a certain explanation please let me know. If you have understood the explanation but think it is an incorrect model of debating please let me know as well to improve the model.

Agreement about the metric

If there is agreement about the metric both teams argue that the motion would change the world along one moral metric, they merely disagree on the sign of the change, i.e. gov says it would change the world to the positive and opp says it would change to the negative. In the motion “THB the US should intervene militarily in Syria” both teams might, for example, agree that the question of the debate is whether more or less war occurs. This makes the life of the adjudicators easier since they merely have to compare the distribution of the two teams and whoever has the higher expected value in their respective direction wins. To illustrate this more clearly we consider the following three scenarios:

• Scenario 1: The opposition’s argument is further in the negative than the government is in the positive with their respective arguments. Therefore, the opposition team wins this clash.
• Scenario 2: The opposition’s argument is less in the negative than the government is in the positive with their respective arguments. Therefore, the government team wins this clash.
• Scenario 3: The opposition’s argument is as far in the negative as the government is in the positive with their respective arguments. We cannot resolve this clash on its own but need to include other information such as their other arguments, their POIs, their responsiveness to that team, the order of the teams in the debate, etc.

If the teams agree on a metric that makes the life of the adjudicators easier - we just compare the sizes of the different effects on the agreed-upon metric. Obviously, there still might be disagreement about whether the teams actually showed this particular effect but it is still easier compared to a situation where multiple metrics have to be weighed against each other.

Disagreement about the metric

In many debates, we have a situation where arguments are based on different philosophical principles, e.g. a Utilitarian calculus, fairness, justice, rights, etc. Often those are not easily translatable into each other and therefore we cannot just “count” their difference towards zero and compare. Therefore we have to weigh the different metrics compared to each other. We could choose to weigh every metric uniformly. However, this would introduce the problem that it would be rational to just spam as many different arguments as possible as long as they are based on different metrics. This is clearly not how we want debating to be and I, therefore, propose to use a “meta distribution” that represents our belief about the strength of the different metrics in the debate. This distribution, similar to the other distributions we have used so far, has a prior that represents the AIVs moral beliefs in a debate and is updated through the arguments made in the debate. The meta distribution is combined with the posteriors of the arguments made in the debate similar to how we combine the truth and relevance distribution, i.e. a high value for your category in the meta distribution implies that the clash that argument is based on is very relevant in the debate and should count a lot.

To illustrate the meta distributions and how they interact with the posteriors of the arguments, consider the following examples. The first is based on a scenario in which the debate revolves around two clashes and the second is used to illustrate three clashes. I also want to point out that meta distributions have priors but I decided not to show them in the illustrations because it would make them too messy. So for the illustrations, we can assume that the presented meta distributions are the posteriors of the meta priors and the arguments that the teams provided during the debate. Arguments to shift our meta distributions are sometimes implicitly presented through framing but often explicitly stated by the second speaker of a team. A team might, for example, argue that their metric is more important than another metric by explaining why one is a logical necessity for the other (i.e. the right to life is a logical necessity for all other rights) or by a thought experiment that distills the metrics of the debate (i.e. whether a person should be allowed to be bind to your body for 9 months if that was the only way they could survive). There are, of course, many other ways to shift meta distributions but I just wanted to give these two from the abortion debate to illustrate the idea.

Two metrics

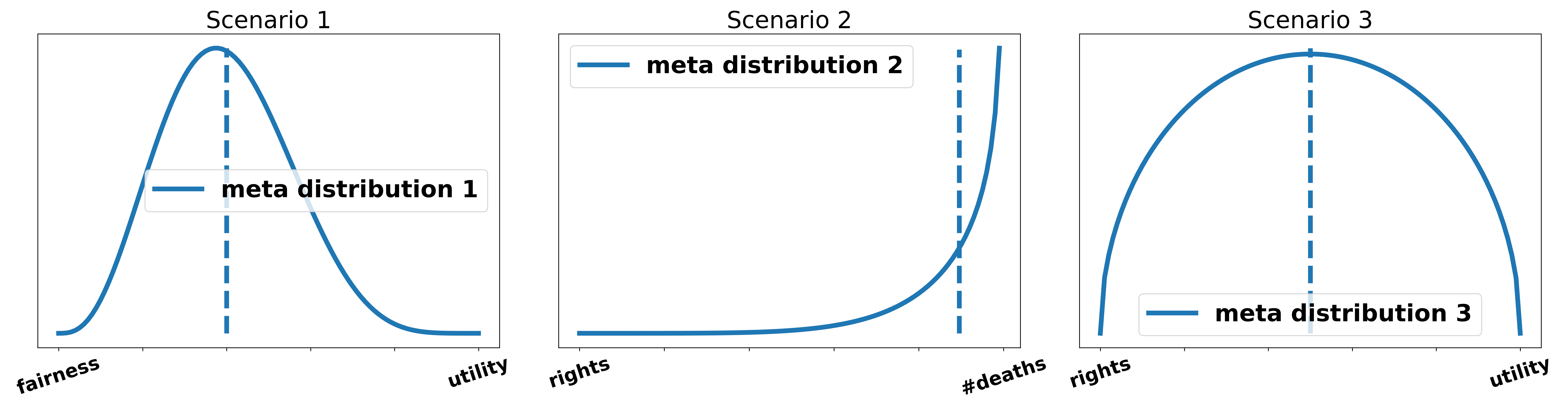
For this example, we consider three debates where the teams agree on two different metrics but found no way to translate them into each other meaningfully.

• Scenario 1: The government team in the debate makes a fairness argument. The opposition makes an argument using a utilitarian calculus. The teams justify their arguments in such a way that our meta distribution after the debate favors the fairness argument by ca. 60:40 as shown in the left subfigures. After combining the posterior distribution we conclude that even though the meta distribution favors the fairness argument the posterior of the utility argument is more persuasive than the posterior of the fairness argument and the opposition team using the utility argument slightly wins the debate.
• Scenario 2: The government team argues a rights metric, i.e. humans should have the right for something independent of the consequences. The opposition argues that due to that measure many people would die. The government team provides a very powerful argument for their case leading to a very high posterior. However, the opposition gives a lot of good reasons why we should consider the number of deaths more than the violation of rights and the government fails to respond to any of them. Therefore, the meta distribution very heavily shifts in favor of the number of deaths. The combination of the respective posterior distributions and the meta distribution yields the distribution shown in the middle subfigures. So even though the government team has a potentially more powerful argument, they fail to respond and lose the debate.
• Scenario 3: The government uses a utilitarian argument. The opposition responds to this with a utilitarian argument themselves but is unable to win this clash on its own. The opposition additionally argues on a rights-based metric. They both do not argue at all for why any of the clashes is more important and we, therefore, have a very uncertain meta distribution over the two metrics. However, our prior does not favor any of the two given the motion and therefore we weigh them equally as shown in the right subfigures. After combining the posteriors with the meta prior we reach a situation in which the opposition is not able to beat the government on any of the two metrics but the combination of both is able to beat the contribution of the government. Therefore, opposition wins.

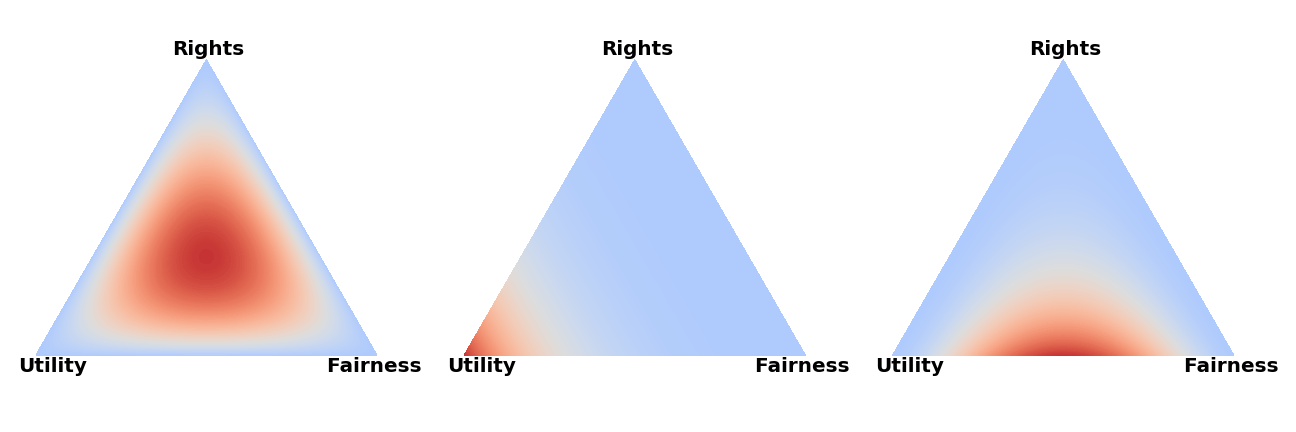
Three metrics

The following scenarios can be seen as the same debate taking place in three different rooms. For simplicity, we assume the teams make the exact same arguments in every debate only differing in their argumentation w.r.t. the metric, i.e. shifting the meta distribution. To simplify even further we also assume that the government team always runs a utilitarian case and the opposition a fairness and a rights case.

• Scenario 1: The teams provide equal justifications for all respective metrics and our meta distribution is therefore agnostic. After combining meta distribution and posteriors we end up with a situation in which the combined arguments from opposition beat the contribution from government and therefore opposition wins.
• Scenario 2: The government team provides strong reasons for why we should care more about the utilitarian calculus than the rights or fairness metric. The opposition does not justify their respective metrics in a very strong manner. Our meta distribution is therefore shifted very strongly in favor of the utilitarian calculus and after combining the posteriors of the arguments and the meta distribution the government team wins.
• Scenario 3: The government team argues that utility is important compared to the other two metrics. The opposition responds by arguing that fairness is important as well but forgets to argue why we should care about their rights case. Therefore their rights argument does not have a lot of weight in the overall consideration. After combining posteriors of the arguments and meta distribution we find that the fairness case of the opposition is able to beat the utility case of the government on its own, the underdeveloped rights case is merely a small addition for the opposition team.

What about the priors?

Similar to part I, we inevitably get to the question of priors again. I think meta priors are a more controversial topic than the priors for the truth and effect distribution since they are impossible to verify empirically, i.e. we cannot truly know whether Utilitarianism, a fairness approach or any other philosophical stance is correct while we can to some extend approximate the truth or relevance of a given statement. It is also harder to evaluate to what extend the “average informed voter” (AIV) believes in any philosophical stance. I think a good starting points for this is the 2012 article by Shengwu Li which was summarized by Stefan Torges in their 2017 article (in German) as follows:

• Freedom, Happiness, and Life are valuable.
• Democracy, Freedom of speech and Equality are important societal principles. However, they are not axiomatic and therefore alterable.
• Laws that restrict the actions of individuals that only affect that individual and nobody else needs a strong justification.
• Important moral questions should be solved through societal discourse and not through reference to (divine) authority.

All of these are not axiomatic - a debate about technocracy has to argue against democracy and there has to be a reasonable chance for the teams defending technocratic governments to win. However, they are good as general normative priors for the judges to have. It is also important to point out that the normative/meta priors are different between motions. I assume that the motion “THW set the voting age to 16” would invoke questions of democratic principles and overall happiness of a population in most AIVs more than questions regarding religious rights. On the other hand, the motion “THW forbid circumcision” very much invokes a question of religious rights and individual happiness but less of democratic principles. That, by no means, implies that people could not argue for these clashes to be important in the debate - it just means that, on average, the AIVs prior assigns them less probability mass.

Imbalanced motions

Imbalanced motions carry a problem that is, again, reducible to the Shift vs Distance to zero debate. Assume, for example, that a motion is gov-heavy and therefore the AIVs prior is +10 for the government. The OG makes arguments that give them +25 persuadability and the OO convince you with +30. In the shift metric, this would mean that OO wins since 30 > 25. In the absolute distance metric, OG would win since 25 + 10 > 30. I think there is a small improvement for the situation that feels a bit hacky. Judges should always assume that the motion is balanced even if they personally think it isn’t. Maybe you are not yet seeing an argument or you have a personal bias. The imbalance would still show since it might be easier for one team to persuade the judges but at least this would make sure that the two metrics yield similar results.

Limitations of the model

I think there are many concepts that we use in debating that have a large effect on a team’s chances to win but are hard to incorporate explicitly rather than implicitly into the model. Within debating we often ask questions like “Does a team meet the correct burden?” or “Did a team meet the right comparative?”. These things are implicitly included in the framework through the relevance or the meta distribution. However, they are not encoded explicitly through additional distributions or assumptions. I am pretty sure that burdens and comparatives could be modeled using more sophisticated statistical models but I don’t know how. If somebody has ideas, I would be very interested. I assume that this book would be a good start.

Conclusions

1. The model is able to integrate most of the relevant parts of debating. At least for a basic illustration, it seems sufficient.
2. It forces you to think about some of the assumptions that we make in more detail. I, for example, always assumed to know exactly what is meant by “rebuttal is to be judged as constructive” but when trying to explain it within the framework I struggled. I think it is also helpful in showing the influence of the priors of the AIV and how it is changed through the debate.
3. Even though some aspects of the real world are explained well, some others have to be bent a bit to fit the debating framework. The fact that priors for the relevance and truth distribution are very skeptical for example, is rather untrue for most people. The AIV would be sufficiently swayed by a couple of lose sentences that carry some conclusion. They would probably not need three separate arguments with 4 mechanisms for each. This would imply that if an opening team does a little bit of intuition pumping for a given argument and thereby already increases their truth distribution to have an expected value over 50 percent no backbench team could run an analysis extension successfully even when they present ten good reasons. Therefore we have to artificially increase the judge’s skepticism to make the probabilistic framework work.
4. I actually think that a lot of disagreements in adjudication can be reduced to the Prior shift vs. Distance to zero debate. The way rebuttal and extensions are judged are definitely very dependent on your stance regarding this question. Unfortunately, I think both positions are to some extend valid and am unable to solve the debate.

Nerd section: some statistical explanations

• The meta distribution is distributed on an N-dimensional probability simplex. In 2D that can be done by a Beta distribution similar to the truth distribution in parts I and II. For 3D I chose to use the Dirichlet distribution which is the higher dimensional equivalent of the Beta distribution (In fact, the Beta is the low-dimensional special case of the Dirichlet). However, all distributions that are on the probability simplex are valid. We could, for example, also chose the logitNormal or even a multimodal distribution.
• To combine the meta distribution with the posterior of the other distributions I used the expected value of the meta distribution and multiplied it with the value determining the posteriors. This is similar to the combination of the truth and relevance distribution in part I and part II.

Acknowledgements

I want to thank Julian, Samuel, Bea, Maria, Marion and Anton for the fruitful discussions, elaborate feedback and grammar-nazi skills (probably still contains some typos though).

One last note:

If you have any feedback regarding anything (i.e. layout or opinions) please tell me in a constructive manner via your preferred means of communication.